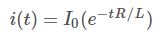本文主要内容:
1、电感充放电过程
2、其串联电阻R=0的电感方程
3、第一个稳态拓扑,升降压拓扑
严格来说,电感不存在充放电,电感只是存在自感电压,这里说充放电比较好理解。
先看一个问题:
1、我们都知道,电感充电时电流是随时间推移而逐渐增加,为什么?
答案:电感电流初始值为零,刚一上电瞬间,电流想突变,感应电压介入,试图让电流重回0,这时感应电压为电源电压。也可推断出,上电瞬间,其串联电阻两端电压为0。那为什么电流会逐渐增加?(看样子外加电压慢慢干掉了感应电压~)
因为,只要存在感应电压,那么电感电流肯定是变化的,而且只能朝着增大的方向变化;这时其串联电阻上产生了压降,电感感应电压就会越来越小~
注:有串联电阻R,电感电流增大的斜率非固定,呈指数形式;而无串联电阻R,其增大的斜率固定,呈直线,下文会介绍到。
1、电感充放电过程
电感充电方程(R≠0):
先看一张图:
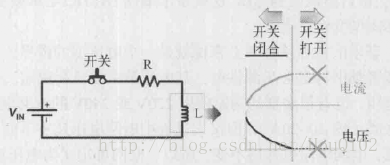
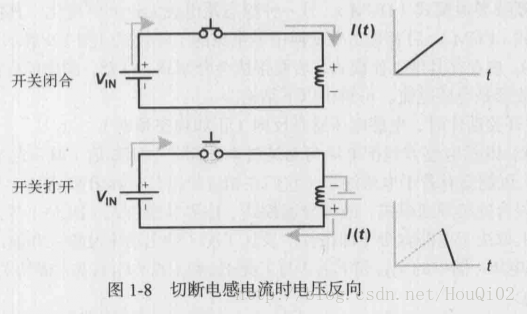
在开关闭合阶段,如充电方程所示,电感电流以指数规律上升,其两端电压以指数规律下降。
这里串联电阻R对时间常数(τ=L/R)的影响
充电阶段:相同供电电压,R越大,到达时间常数点(电流最终值的63%)越快
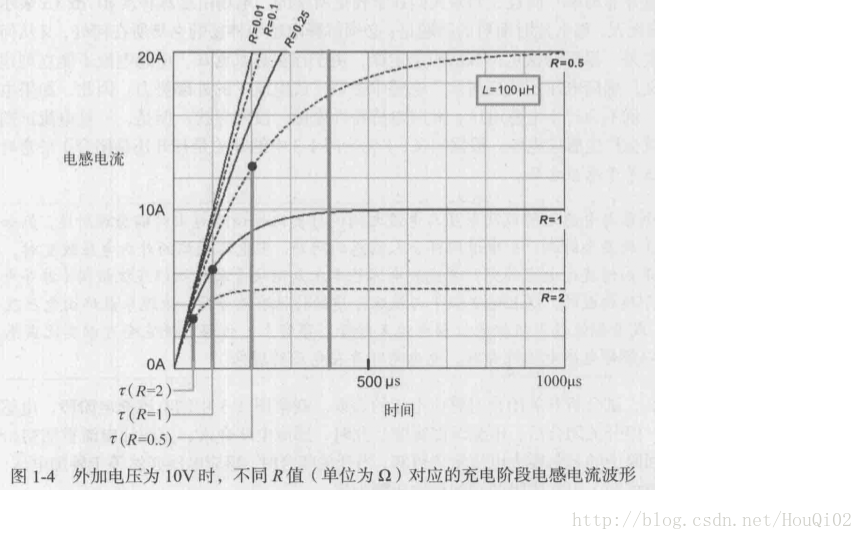
放电阶段:相同供电电压,R越大,到达时间常数点(电流初始值的37%)越快
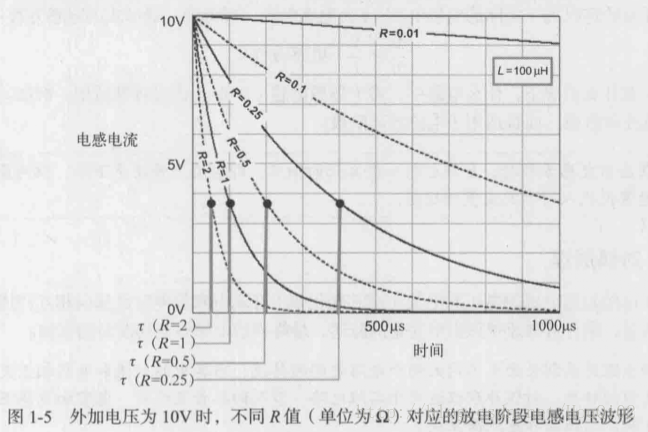
电感放电方程(R≠0):
在开关断开阶段,电感电流以指数规律下降;其开关触点两端会出现一个电弧(电压尖峰),如果触点距离增加,电感感应电压会增加以维持电弧(电流)的存在。
2、其串联电阻R=0的电感方程
题外话:为什么要讲这个方程?说白了,因为我们接下来的开关拓扑分析,没有串联电阻R(R=0)。这对我们接下来的电感充电和放电斜率理解有帮助
在开关导通阶段,电感电压从初始值VIN 开始变化,唯一的原因就是电阻R的存在。所以,当R=0时,电感电压不会变化,感应电压等于外加直流电压。(只要电感电流持续变化,该电压就能保持住,再来句废话,就是只要电感两端存在电压,其电流必有变化)
当电阻较小时,电感电流以恒定的斜率上升或下降,如图1-4和1-5
3、第一个稳态拓扑,升降压变换器
这里我们一步一步来
玛尼克塔拉说,对待电感感应电压尖峰的问题,要么不管他,要么就压制他~
好吧,一个二极管成功解决~
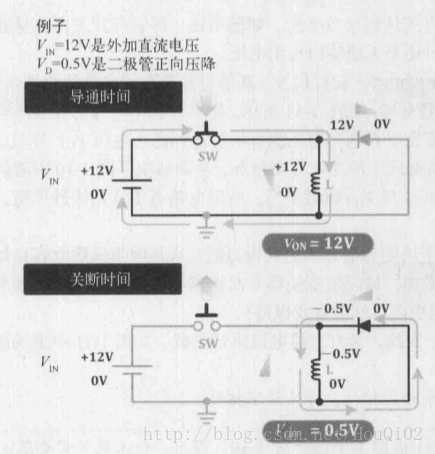
下面我要用白话文了来讲解了~
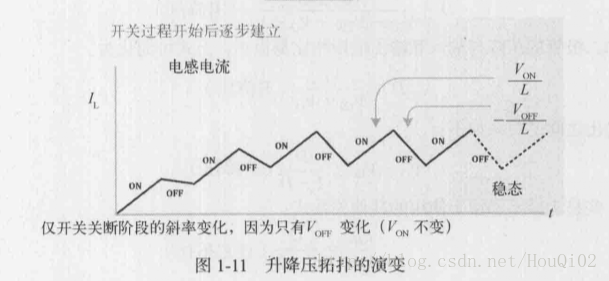
上图电感电流上升斜率是VON/L ,下降斜率是VOFF/L ,明显VOFF 的斜率要小于VON ,那么如果VOFF 时间不够电感复位(电感放电完毕),就会出现下图的情况,电流呈阶梯式上升,简称非稳态:
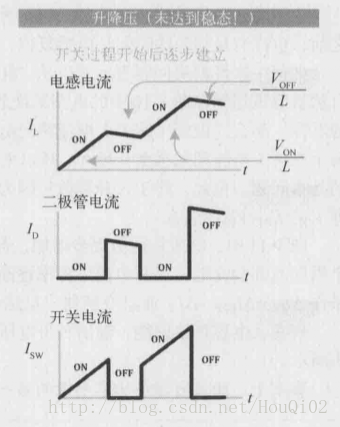
既然都出现非稳态了,那我们就要让他稳态起来:
首先想一想稳态的条件,当VON 和VOFF 幅值差不多时,占空比0.5,最容易达到稳态,差太多那就不好办了
那有什么既便宜又好用的方法呢?加个电容
如果让电感放电电流继续给电容充电,电容电压就会达到稳态电压VO ,这样,电感电压就会有升高的空间了,电流下降率随之下降。
若干个周期之后,电感电流IL 就会达到稳态值了。此时电容虽然每个周期都会充电,但其电流下降率逐渐增加,最终自然稳定在固定输出电压了。(占空比固定,是多少,下文计算)
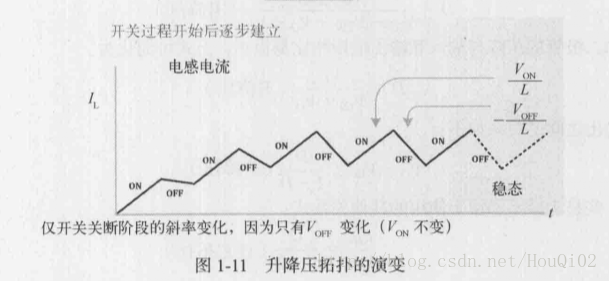
计算占空比
这里我们假设输出电压最终稳定在5V。
电感是非耗能器件,应用伏秒定律(电压*时间):
故,需稳定输出5V(达到伏秒平衡),关断时间必须是导通时间的2.18倍。
可得D=0.314
推导出升降压拓扑
下图为升降压拓扑电路:
由上图可知:
OK,升降压变换拓扑推到出来了(注意这里的升降压是正对负输出的)
如有描述不当和错误的地方,恳请看官提出交流,谢谢~
后续会继续介绍剩余两种拓扑,升压和降压
本文转载自:后起的博客