我们已经知道交流电有以下性质:
1.大小和方向均做周期性变化,平均值为零;有三要素:幅值、角频率、初相位;
2.描述交流电的方式有瞬时值表示法、波形图、有效值、矢量法;
3.不同的交流电之间可能同相、反相、正交,或者相差某个角度;
4.交流电通过电阻、电感、电容以及它们的组合电路,所表现出来的性质不同,主要反映在相位、阻抗、功率上;
以上四点和直流电均不同,因此交流电在计算上有自己的公式、方法、性质。
好了,回顾了上述问题之后就可以进行以下学习了;电阻、电感、电容的差别之处在以下6个方面,我们逐一进行讲解,对比。
一、电阻
1.瞬时值关系式:u=RI,也就是通过电阻的电压等于通过的电流与电阻的乘积,注意这个公式里面的u、i均是小写;这个公式中实际使用当中很少用到,它反映的是电压和电流的瞬时值关系;
2.有效值关系:电阻等于电压与电流的比值,注意这里的电压和电流均是有效值,这个是非常实用的公式,我们应该掌握,它和直流电路的计算方式是一样的;
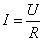
3.阻抗:电阻的阻抗就是电阻,怎么听起来这么别扭呢?我们前面讲过,阻抗包括电阻、感抗、容抗,是针对不同的电抗元件而言的,这是交流电特有的;

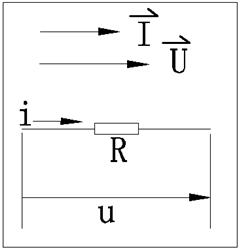
4.矢量图,从图上可以看出,加在电阻上的电压和电流是同相关系;
5.功率,等于电压与电流的积,或者电流的平方与电阻的积,P=UI,单位瓦特(W),这个功率叫有功功率,就是实实在在的消耗了电能的功率,这是电阻特有的,它就是一个耗能元件;
6.功率因数:我们知道功率因数就是电压和电流相位差的余弦,由于加在电阻上的电压和电流同相,即相位差为零,那么其功率因数就是cosφ=1,这是最大值;
二、电感L
1.瞬时值关系
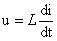
也就是加在交流电上的电压与电流的变化率成正比,注意和电阻的瞬时值一样u、i均是小写;这个公式有价值,应记住;另外是与变化率成正比,不是变化量也不是固定值,这与电阻不同;
2.有效值关系:加在电感上的电流与电压成正比,等于感抗,注意电压电流均是有效值,这个是非常实用的公式,我们应该掌握,它和电阻在形式上一致;
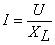
3.阻抗:电感对电流有阻碍作用,其值的大小用感抗表示XL=2πfL,f交流电的频率,L电感;从该公式可以看出,交流电频率越大,电感对其感抗越大,这就是交流电的通直隔交作用,用它的这个功能可以进行滤波;
4.矢量图:从图上可以看出,加在电感上的电压超前于电流90°
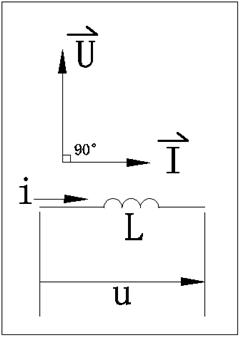
5.功率,有功功率P=0,也就是电感的有功功率为零,它不是耗能元件,它是储能元件,其储能能力用无功功率表示QL=UI,等于电压与电流的积,或者电流的平方与感抗的积,,单位乏尔(var),这是其重要特点;
6.功率因数:由于加在电感上的电压超前于电流90°,也就是二者的相位差90°,那么cosφ=0;
三、电容C
1.瞬时值关系
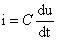
也就是通过电容的电流与其两端的电压的变化率成正比,注意和电阻的瞬时值一样u、i均是小写;这个公式有价值,应记住;
2.有效值关系:加在电容上的电流与电压成正比,等于容抗,注意这里的电压、电流均是有效值,这个是非常实用的公式,我们应该掌握,它和电阻、感抗的计算式在形式上一致;

3.阻抗,电容和电阻、电感一样,也对电流有阻碍作用,其值的大小用容抗表示,f交流电的频率,C电容,通过这个公式我们可以看出,交流电的频率越大,容抗越小,直流电频率为零,容抗无限大,这就是电容的隔直通交作用。
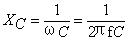
4.矢量图,从图上可以看出,加在电容上的电压滞后于电流90°
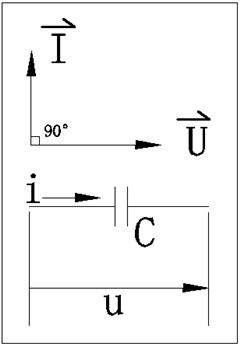
5.功率,P=0,也就是电容和电感的有功功率均为零,它也不是耗能元件,它和电感一样是储能元件,其储能能力用无功功率表示QL=UI,等于电压与电流的积,或者电流的平方与容抗的积,,单位也是乏尔(var),
6.功率因数,由于加在电容上的电压超前于电流90°,也就是二者的相位差90°,那么cosφ=0;
通过以上的分析,我们看出交流电通过电阻、电感、电容所表现出来的性质大不相同,正是这种差异,使得它们的组合性质多样化,表现出了丰富多彩的性质,在电子电路中得到了广泛的应用,比如选频、移相等。
文章来源:电工电子diy
